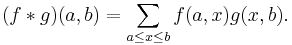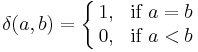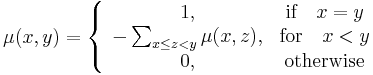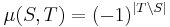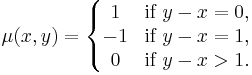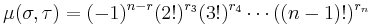Incidence algebra
In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered set and commutative ring with unity.
Contents |
Definition
A locally finite poset is one for which every closed interval
- [a, b] = {x : a ≤ x ≤ b}
within it is finite.
The members of the incidence algebra are the functions f assigning to each nonempty interval [a, b] a scalar f(a, b), which is taken from the ring of scalars, a commutative ring with unity. On this underlying set one defines addition and scalar multiplication pointwise, and "multiplication" in the incidence algebra is a convolution defined by
An incidence algebra is finite-dimensional if and only if the underlying poset is finite.
Related concepts
An incidence algebra is analogous to a group algebra; indeed, both the group algebra and the incidence algebra are special cases of a categorical algebra, defined analogously; groups and posets being special kinds of categories.
Special elements
The multiplicative identity element of the incidence algebra is the delta function, defined by
The zeta function of an incidence algebra is the constant function ζ(a, b) = 1 for every interval [a, b]. Multiplying by ζ is analogous to integration.
One can show that ζ is invertible in the incidence algebra (with respect to the convolution defined above). (Generally, a member h of the incidence algebra is invertible if and only if h(x, x) is invertible for every x.) The multiplicative inverse of the zeta function is the Möbius function μ(a, b); every value of μ(a, b) is an integral multiple of 1 in the base ring.
The Möbius function can also be defined directly, by the following relation:
Multiplying by μ is analogous to differentiation, and is called Möbius inversion.
Examples
- Positive integers ordered by divisibility
- The Möbius function is μ(a, b) = μ(b/a), where the second "μ" is the classical Möbius function introduced into number theory in the 19th century.
- Finite subsets of some set E, ordered by inclusion
- The Möbius function is
- whenever S and T are finite subsets of E with S ⊆ T, and Möbius inversion is called the principle of inclusion-exclusion.
- Geometrically, this is a hypercube:
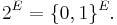
- Natural numbers with their usual order
- The Möbius function is
- and Möbius inversion is called the (backwards) difference operator.
- Geometrically, this corresponds to the discrete number line.
- Recall that convolution of sequences corresponds to multiplication of formal power series.
- The Möbius function corresponds to the sequence (1, −1, 0, 0, 0, ... ) of coefficients of the formal power series 1 − z, and the zeta function in this case corresponds to the sequence of coefficients (1, 1, 1, 1, ... ) of the formal power series
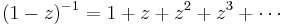 , which is inverse. The delta function in this incidence algebra similarly corresponds to the formal power series 1.
, which is inverse. The delta function in this incidence algebra similarly corresponds to the formal power series 1.
- Subgroups of a finite p-group G, ordered by inclusion
- The Möbius function is
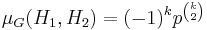 if
if 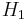 is a normal subgroup of
is a normal subgroup of 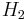 and
and 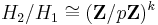
- and it is 0 otherwise. This is a theorem of Weisner (1935).
- Finite sub-multisets of some multiset E, ordered by inclusion
- The above three examples can be unified and generalized by considering a multiset E, and finite sub-multisets S and T of E. The Möbius function is
- This generalizes the positive integers ordered by divisibility by a positive integer corresponding to its multiset of prime divisors with multiplicity, e.g., 12 corresponds to the multiset
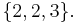
- This generalizes the natural numbers with their usual order by a natural number corresponding to a multiset of one underlying element and cardinality equal to that number, e.g., 3 corresponds to the multiset
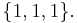
- Partitions of a set
- Partially order the set of all partitions of a finite set by saying σ ≤ τ if σ is a finer partition than τ. Then the Möbius function is
- where n is the number of blocks in the finer partition σ, r is the number of blocks in the coarser partition τ, and ri is the number of blocks of τ that contain exactly i blocks of σ.
Euler characteristic
A poset is bounded if it has smallest and largest elements, which we call 0 and 1 respectively (not to be confused with the 0 and 1 of the ring of scalars). The Euler characteristic of a bounded finite poset is μ(0,1); it is always an integer. This concept is related to the classical Euler characteristic.
Reduced incidence algebras
Any member of an incidence algebra that assigns the same value to any two intervals that are isomorphic to each other as posets is a member of the reduced incidence algebra. This is a subalgebra of the incidence algebra, and it clearly contains the incidence algebra's identity element and zeta function. Any element of the reduced incidence algebra that is invertible in the larger incidence algebra has its inverse in the reduced incidence algebra. As a consequence, the Möbius function is always a member of the reduced incidence algebra. Reduced incidence algebras shed light on the theory of generating functions, as alluded to in the case of the natural numbers above.
See also
Literature
Incidence algebras of locally finite posets were treated in a number of papers of Gian-Carlo Rota beginning in 1964, and by many later combinatorialists. Rota's 1964 paper was:
- Rota, Gian-Carlo (1964), "On the Foundations of Combinatorial Theory I: Theory of Möbius Functions", Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 2 (4): 340–368, doi:10.1007/BF00531932
- N. Jacobson, Basic Algebra. I, W. H. Freeman and Co., 1974. See section 8.6 for a treatment of Mobius functions on posets